第二章线性表 - 《数据结构导论》笔记

概要

线性表
1. 概念
2. 特征
3. 基本运算的功能描述
  - 初始化
  - 求表长
  - 读取元素
  - 定位
  - 插入
  - 删除
线性表的顺序存储结构——顺序表
1. 概念
2. 用C语言描述
3. 运算实现的关键步骤和算法
  - 容量
  - 表长
  - 插入
  - 删除
  - 定位
4. 应用
  - 实现简单算法
  - 算法实现的分析
线性表的链式存储结构——单链表
1. 特点和结构
2. 基本概念
  - 头指针
  - 头结点
  - 首结点
  - 尾结点
  - 空链表
3. 用C语言描述
4. 运算实现的关键步骤和算法
  - 插入
  - 删除
  - 定位
5. 综合应用
  - 设计算法解决应用问题
顺序表和链表的优缺点、适用场景
循环链表和双向循环链表
1. 特点和结构
2. 用C语言描述
3. 基本运算
  - 插入
  - 删除

线性表

概念

线性表Linear List是一种线性结构，它是由n（n ≥ 0）个数据元素组成的有穷序列，其中：

数据元素又称为结点。
这里的n代表线性表的总结点个数，又称为表长。
当表长为0时，也就是线性表没有任何结点，称为空表，用 () 或 Ø 表示。
线性表通常表示成：(A1, A2, A3, ..., An)，其中：
- A1称为起始结点。
- An称为终端结点。
- A1是A2的直接前驱，A3是A2的直接后继，其他结点同理。

特征

线性表中结点之间具有一对一的关系。
非空表的情况下：
- 除了起始结点没有直接前驱（例：A1），其他的结点有且仅有一个直接前驱（例：A2、A3等）。
- 除了终端结点没有直接后继（例：An），其他的结点有且仅有一个直接后继（例：A1、A2等）。

基本运算的功能描述

以下的no指的是序号，文中所有提到的“位置”都是指序号。

避免用i命名是怕和数组的下标混在一起，数组的下标是从0开始，而序号是从1开始。

初始化Initiate(L)：建立一个空表L=()，L不包含任何结点。
求表长Length(L)：返回线性表L的长度，以下简称表L。
读取元素Get(L, no)：返回表L的第no个结点，当no超出Length(L) ≥ no ≥ 1范围，返回一特殊值。
定位Locate(L, x)：返回表L中第一个结点的值等于x值的序号，如果找不到则返回0。
插入Insert(L, x, no) ：两个步骤。
- 在表L的第no个结点之前插入一个新结点x，no的合法范围：Length(L) + 1 ≥ no ≥ 1。
- 表长度加1。
删除Delete(L, no)：两个步骤。
- 删除表L的第no个结点，no的合法范围：Length(L) ≥ no ≥ 1。
- 表长度减1。

顺序表

概念

顺序存储：将结点依次存放在计算机内存中一组连续的存储单元中，逻辑结构中相邻的结点它的存储位置也相邻。
顺序表：用顺序存储实现的线性表，一般使用数组来表示顺序表。

用C语言描述

假设线性表的数据元素的类型为DataType，顺序表的结构定义如下：

1
2
3
4
5
6
7


const int Maxsize = 100; // 预先定义一个足够大的常数
typedef struct
{
	DataType data[Maxsize]; // 存放数据的数组
	int length; // 顺序表的实际长度
} SeqList; // 顺序表类型名为SeqList
SeqList L; // 定义L为一个顺序表

例如：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


const int Maxsize = 7; // 预先定义数组大小
typedef struct
{
	int num; // 学号
	char name[8]; // 姓名
	int age; // 年龄
} DataType; // 定义结点的类型
typedef struct
{
	DataType data[Maxsize]; // 存放数据的数组
	int length; // 线性表的实际长度
} SeqList; // 顺序表的类型
SeqList student; // student是顺序表的名称

运算

以下相关运算的代码已经整理好，放在了ghjayce/code-example - sequence list中，感兴趣的话可以clone到本地查看运行结果。

插入

算法：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


SeqList insertSeqList(SeqList L, DataType x, int no)
{
    if (L.length >= Maxsize) {
        printf("%s\n", "表已满");
        exit(EXIT_FAILURE);
    }
    // 等同于：no <= 0 || no >= L.length + 2
    if (no < 1 || no > L.length + 1) {
        printf("%s\n", "插入位置不正确");
        exit(EXIT_FAILURE);
    }
    for (int i = L.length; i >= no; i--) {
        L.data[i] = L.data[i - 1];
    }
    L.data[no - 1] = x;
    L.length++;
    return L;
}

步骤：

检查插入位置是否合法。
1. 表容量，表满了以后不能再插入。
2. 插入位置：
  - 不能插入序号no = 0及之前的位置，no = 1的位置可以插入。
  - 要插入的位置，它前面的位置不能是空的，也就是不能断开插入。
    - 例：插入第5个位置，第4个位置是空的。
为插入位置腾出空位，从最后一个结点开始从后往前循环，将结点往后移一个位置，直到插入位置结束。
插入新的结点x，也就是序号no的位置，对应下标为：no-1。
表长度加一。

分析：

算法复杂度：O(n)。
平均移动次数：$\frac{n}{2}$。

插入算法中，元素的移动次数不仅与顺序表的长度n有关，还和插入的no位置有关：

当插入位置是n+1时，移动次数为0。
当插入位置是n时，移动次数为1，这个称为首项（从存在的元素中选取，它也可以是尾项）。
当插入位置是n-1时，移动次数为2。
当插入位置是n-2时，移动次数为3。
…
当插入位置是1时，移动次数为n，这个称为末项。

根据移动次数变化的规律可以看出：

比较和移动次数的计算方式为：n - no + 1。
可插入的位置有：n + 1个。
这是个等差数列。
- 使用高斯求和公式可以得出总的移动次数为：$\frac{(n + 1) \times n}{2}$。
- 因此平均移动次数：$\frac{总移动次数}{可插入位置}$也就是$\frac{\frac{(n + 1) \times n}{2}}{n + 1}$约为$\frac{n}{2}$。

如果我有理解错平均移动次数，请大佬随时斧正，联系我。

删除

算法：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


SeqList deleteSeqList(SeqList L, int no)
{
    // 等同于：no <= 0 || no >= L.length + 1
    if (no < 1 || no > L.length) {
        printf("%s\n", "非法位置");
        exit(EXIT_FAILURE);
    }
    for (int i = no; i < L.length; i++) {
        L.data[i-1] = L.data[i];
    }
    L.length--;
    return L;
}

步骤：

检查删除位置是否合法，不能是0及之前的位置，也不能是超出表长之后的位置。
覆盖结点，从删除位置开始，后一个结点移动到前一个位置，直到最后一个结点结束，即表示删除。
表长度减一。

分析：

算法复杂度：O(n)。
平均移动次数：$\frac{n-1}{2}$。

跟插入算法一样：

当删除位置是n时，移动次数为0。
当删除位置是n-1时，移动次数为1。
当删除位置是n-2时，移动次数为2。
…
当删除位置是1时，移动次数为n-1。

根据规律得出：

移动次数的计算方式：n - no。
可删除的位置有：n个。
同样是等差数列。
- 使用高斯求和公式得出总的移动次数：$\frac{(0 + n - 1) \times n}{2}$。
- 平均移动次数：$\frac{总移动次数}{可删除的位置}$也就是$\frac{\frac{(0 + n - 1) \times n}{2}}{n}$约为$\frac{n-1}{2}$。

如果我有理解错平均移动次数，请大佬随时斧正，联系我。

定位

算法：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


int locateSeqList(SeqList L, DataType x)
{
    int i = 0;
    // 为了简化运算，这里只比对DataType里的id
    while ((i < L.length) && (L.data[i].id != x.id)) {
        i++;
    }
    if (i < L.length) {
        return i + 1;
    }
    return 0;
}

步骤：

初始化一个下标值：0。
从头到尾逐个比对，数组中的结点是否与结点x相等：
1. 不相等则继续循环。
2. 相等则表示已经找到，停止循环。
返回查找结果。

表长

只需要返回L.length即可

链表

概念

链表的结点：由数据域（数据元素）和指针域或者叫链域（表示数据元素之间的逻辑关系）组成。
- 数据域：相当于火车厢。
- 指针域：相当于连接火车厢的车钩。
链式存储：各个结点在内存中的存储位置并不一定连续，逻辑结构中相邻的结点其存储位置不一定相邻。
链表：用链式存储实现的线性表，所有结点通过指针链接形成链表Link List，结点之间可以重新链接。
- 单链表：每个结点由一个数据元素和一个指向下一个结点（后继结点）的next指针构成。
- 循环链表：单链表的基础上，尾结点的指针指向首结点。
- 双向循环链表：循环链表的基础上，每个结点增加一个指向上一个结点（前驱结点）的prio指针。
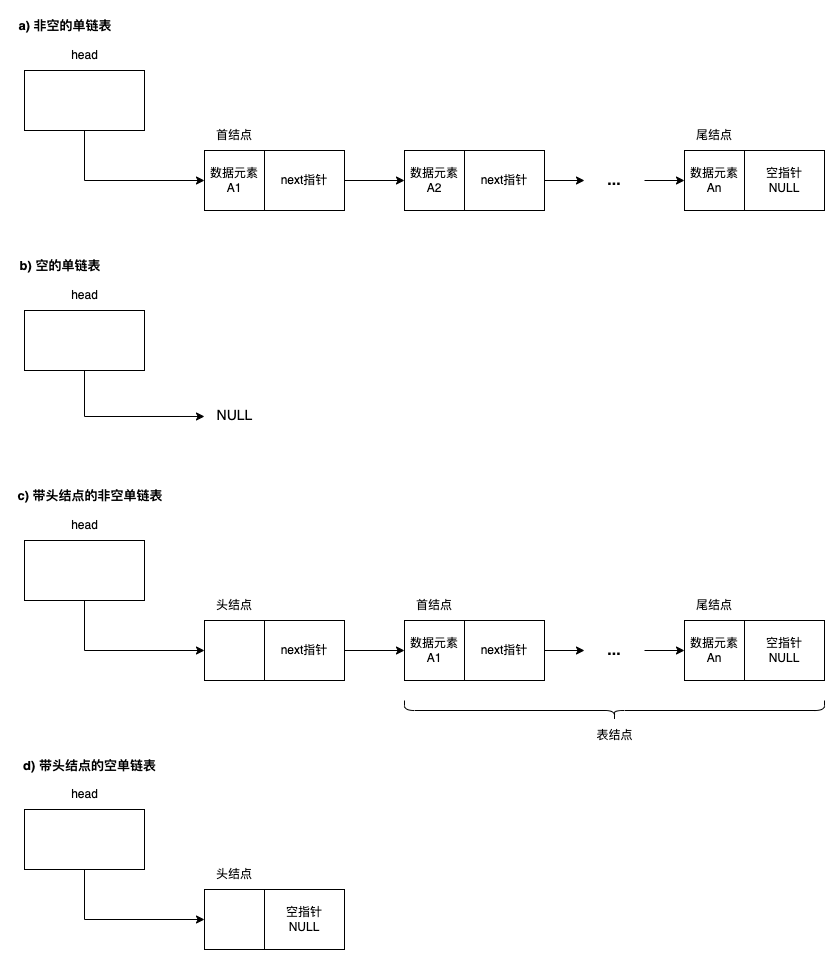
组成介绍：
- head：头指针变量，有两个作用：
  - 它的值指向链表的第一个结点。
  - 也可以用来命名链表，例如下图链表称为：表head、head表。
- 首结点：链表中第一个数据元素结点。
- 尾结点：也称终端结点，指链表中最后一个数据元素结点。
  - 空指针：尾结点的指针域的值为NULL。
- 空链表：head等于NULL，表示链表无任何结点。
- 头结点：为了方便运算，在首结点之前增加一个相同类型的结点，如图C)。
- 表结点：除了头结点以后的结点。

单链表、带头结点的单链表

用C语言描述

1
2
3
4
5
6
7
8


typedef struct node
{
    DataType data;
    struct node *next;
} Node, *LinkList;
// Node，*LinkList都是结构体的别名，其中
// Node是指向struct node类型的别名
// *LinkList是指向Node类型的指针的别名

例如：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


typedef struct
{
	int num; // 学号
	char name[8]; // 姓名
	int age; // 年龄
} DataType; // 定义结点的类型

typedef struct node
{
	DataType data; // 数据域
	struct node * next; // 指针域
} Node, *LinkList; // Node是链表结点的类型
LinkList head; // 定义一个全局变量，head是链表的名称

运算

以下相关运算的代码已经整理好，放在了ghjayce/code-example - link list中，感兴趣的话可以clone到本地查看运行结果。

初始化

1
2
3
4
5
6
7


LinkList initLinkList() // 建立一个空的单链表
{
	LinkList head; // 定义局部变量，头指针
	head = malloc(sizeof(Node)); // 动态构建一结点，它是头结点
	head->next = NULL;
	return head;
}

步骤：

基于LinkList结构，构建一个名为head的单链表。
通过给head分配内存、设置属性，此时head是一个头结点，next指针为NULL，表示链表为空。
返回这个链表的头结点。

求表长

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


int lengthLinkList(LinkList head) // 求单链表head的长度
{
	// 声明一个指向Node对象的名为point的指针变量，它指向head的头结点
	Node *point = head;
	int count = 0;
	while (point->next != NULL)
	{
		point = point->next
		count++;
	}
	return count;
}

步骤：

指向head表的头结点。
初始化count计数。
从head头结点开始，检查头结点的下一个结点，也就是首结点：
1. 结点不为空，此时point变成首结点，计数+1，依次往后检查下一个结点是否为NULL。
2. 结点为NULL结束循环。
返回表长。

读取元素

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


Node *getLinkList(LinkList head, int no) // 读取序号为第no个结点，读到返回结点
{
	Node *point;
	point = head->next;
	int position = 1;
	while (point != NULL && position < no)
	{
		point = point->next;
		position++;
	}
	if (position == no) {
		return point;
	}
	return NULL;
}

步骤：

声明point指针变量，指向head表的首结点。
初始化position，也就是从第一个结点（位置1）开始查找。
检查point结点不能是空的，并且position要小于查找的no。
1. 符合条件，表示还没找到，此时point变成下一个结点，position+1，重复步骤3。
2. 不符合条件，结束循环，分为两种情况，可能遍历完整个链表都没找到或者提前找到了。
判断position是否等于no序号：
1. 相等，表示已经找到，返回point结点。
2. 不相等，表示没有找到，返回NULL值。

定位

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


int locateLinkList(LinkList head, DataType x) // 在head表中找到第一个符合x结点的序号
{
	Node *locateNode;
	locateNode = head->next;
	int no = 1;
	while (locateNode != NULL && locateNode->data != x)
	{
		locateNode = locateNode->next;
		no++;
	}
	if (locateNode == x) {
		return no;
	}
	return 0;
}

关键点：

从首结点开始，当前结点不为空并且不等于要查找的值则继续检查下一个结点：
1. 如果提前找到结点locateNode，循环结束。
2. 如果遍历完链表依然没找到，locateNode等于尾结点，循环结束。
比对locateNode和x：
1. 相等，就是找到了，返回locateNode所在的序号。
2. 不相等，也就是没找到，返回0。

插入

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


LinkList insertLinkList(LinkList head, DataType x, int no)
{
    Node *queryNode, *newNode;
    if (no == 1) {
        queryNode = head;
    } else {
        queryNode = getLinkList(head, no-1);
    }
    if (queryNode == NULL) {
        printf("插入位置有误");
        exit(EXIT_FAILURE);
    }
    newNode = malloc(sizeof(Node));
    newNode->data = x;
    newNode->next = queryNode->next;
    queryNode->next = newNode;
    return head;
}

关键点：

找到要插入位置的前驱结点query：
1. 生成一个新的结点newNode，按照Node结构分配内存。
2. newNode的next要指向query的next，数据域赋值为x也别忘了。
3. query的next指向newNode。
注意如果插入的位置为1，要做处理，避免取一个非法的前驱结点。
要对查找插入位置的结果做处理。
1.2和1.3的步骤不能调换，必须严格执行，不然会丢失query的next结点。

删除

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


LinkList deleteLinkList(LinkList head, int no)
{
    Node *deleteNode, *queryNode;
    if (no == 1) {
        queryNode = head;
    } else {
        queryNode = getLinkList(head, no-1);
    }
    if (queryNode == NULL || queryNode->next == NULL) {
        printf("%s\n", "删除的位置错误");
        exit(EXIT_FAILURE);
    }
    deleteNode = queryNode->next;
    queryNode->next = deleteNode->next;
    free(deleteNode);
    return head;
}

关键点：

和插入有点类似，也得先找到要查删除位置的前驱结点query，当然也要注意非法前驱的处理。
要对查找删除位置的结果做处理。
要删除的结点放到临时变量存起来，目的用于free释放内存空间。
把前驱结点query的next指向删除结点的next即可，如果删除结点是尾结点，那么query的next就是NULL。

创建

为了方便后续算法演示，这里用一个数组来构建单链表，再简化一下DataType的属性：

1
2
3
4
5
6


int nums[6] = {4, 7, 2, 5, 2, 4};

typedef struct
{
	int age;
} DataType;

结合以上已实现的算法initLinkList()和insertLinkList()，实现一个创建链表的算法。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


LinkList createLinkListByEach(int *arr, int size)
{
    LinkList point = initLinkList();
    for (int i = 0; i < size; i++) {
        DataType item;
        item.age = arr[i];
        insertLinkList(point, item, i+1);
    }
    return point;
}
// 调用
// 为了方便展示直接写6，size自动计算：sizeof(nums) / sizeof(nums[0])
createLinkListByEach(nums, 6);

缺点：每次插入结点都要遍历一次链表。

尾插法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


LinkList createLinkListByTailInsert(int *arr, int size)
{
    LinkList head;
    Node *lastNode, *newNode;
    head = malloc(sizeof(Node));
    lastNode = head;
    for (int i = 0; i < size; i++) {
        DataType item;
        item.age = arr[i];

        newNode = malloc(sizeof(Node));
        newNode->data = item;
        lastNode->next = newNode;
        lastNode = newNode;
    }
    lastNode->next = NULL;
    return head;
}

优点：每次插入新结点都能从尾结点进行而不需要每次遍历整个链表。

头插法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


LinkList createLinkListByHeadInsert(int *arr, int size)
{
    LinkList head;
    Node *newNode;
    head = malloc(sizeof(Node));
    head->next = NULL;
    for (int i = 0; i < size; i++) {
        DataType item;
        item.age = arr[i];

        newNode = malloc(sizeof(Node));
        newNode->data = item;
        newNode->next = head->next;
        head->next = newNode;
    }
    return head;
}

与尾插法算法一样，只是插入新结点是从头结点进行，最终链表的顺序与尾插法相反。

删除重复结点

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


LinkList removeRepeatLinkList(LinkList head)
{
    Node *searchNode; // 要查找的结点
    Node *checkNode; // 要检查（比对）的结点
    Node *deleteNode; // 要删除的结点
    searchNode = head->next; // 从首结点开始
    while (searchNode != NULL) {
	// 关键，从首结点开始，循环检查当前结点的下一个结点
        checkNode = searchNode;
        while(checkNode->next != NULL) {
            if (searchNode->data.age == checkNode->next->data.age) {
                deleteNode = checkNode->next;
                checkNode->next = deleteNode->next;
                free(deleteNode);
            } else {
                checkNode = checkNode->next;
            }
        }
        searchNode = searchNode->next;
    }
    return head;
}

关键点：

从首结点开始遍历，取它的值与下一个结点的值进行比较，找到相等的值进行删除。
checkNode=searchNode; while(checkNode->next != NULL)是关键之一。

其他链表

循环链表

带头结点的单链表、带尾结点的循环链表

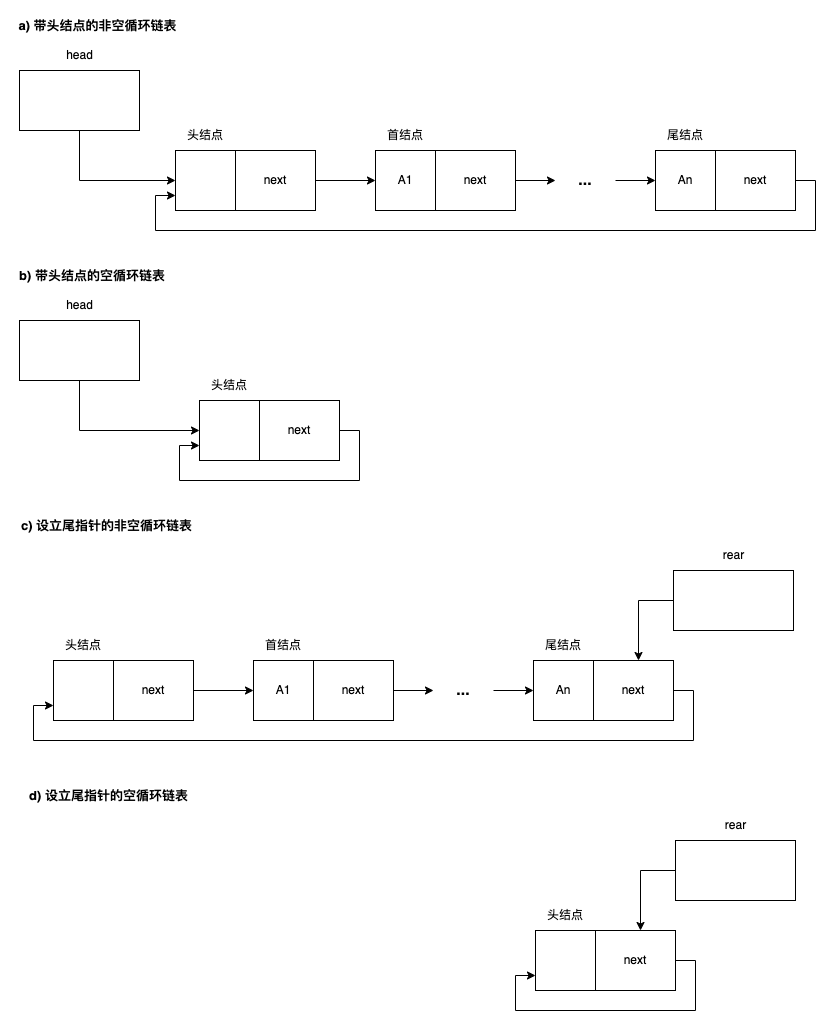
带尾结点访问首结点的表示方式：rear->next->next，运算与单链表类似，不再赘述。

双向循环链表

用类C语言来描述：

1
2
3
4
5
6
7


struct dbnode
{
	DataType data;
	struct dbnode *prior, *next;
}
typedef struct dbnode *dbpointer;
typedef dbpointer DLinkList;

双向循环链表和单链表的运算差不多，主要提一下删除和插入运算的差异。

删除算法的关键点：

1
2
3


removeNode->prior->next = removeNode->next;
removeNode->next->prior = removeNode->prior;
free(removeNode);

第1行和第2行代码顺序颠倒也可以，不影响最终效果。

插入算法的关键点：

1
2
3
4


newNode->prior = query;
newNode->next = query->next;
query->next->prior = newNode;
query->next = newNode;

注意query是指插入位置的前驱结点，以及这些语句的顺序。

先接好新结点的prior和next指针的指向。
再将插入位置结点的prior指针指向新结点。
最后将query结点的next指针指向新结点。

顺序表和链表的比较

异同

存储方式：
- 顺序表：
  1. 使用连续的内存空间来存储结点。
  2. 需要预先分配存储空间，存储结点个数有上限。
- 链表：
  1. 结点由数据元素和指针组成，指针指向下一个结点，存储在内存空间连不连续都可以。
  2. 不需要预先分配存储空间，存储结点个数没有上限。
访问效率：
- 顺序表：
  1. 能根据索引快速定位结点，时间复杂度O(1)。
  2. 读取结点支持随机访问。
- 链表：
  1. 只能通过遍历链表，从头到尾逐个遍历查找目标结点，时间复杂度O(n)。
  2. 读取结点不支持随机访问。
运算（插入和删除）：
- 顺序表：
  1. 插入和删除需要移动后续的结点，以保证结点之间的连续性。
  2. 插入和删除操作之前需要查找定位，时间复杂度O(n)。
- 链表：
  1. 插入和删除只需要修改结点之间指针的指向关系，不需要移动结点。
  2. 跟顺序表一样需要查找定位，时间复杂度也是O(n)。

优缺点

顺序表：
- 优点：
  1. 随机访问效率高。
- 缺点：
  1. 插入和删除的操作代价高。
  2. 需要预先分配一块连续的内存空间。
  3. 存储结点个数有上限。
链表：
- 优点：
  1. 插入和删除的操作代价低。
  2. 对内存空间控制动态且灵活。
  3. 存储结点个数没有上限（取决于可用内存空间）。
- 缺点：
  1. 不支持随机访问。
  2. 相对要占用多一些内存空间来存放指针域。

适合场景

根据上面的优缺点可得知：

顺序表：更适合读多写（插入和删除）少的场景。
链表：更适合写多读少的场景。

综合应用

待补充…

目录

概要

线性表

概念

特征

基本运算的功能描述

顺序表

概念

用C语言描述

运算

插入

删除

定位

表长

链表

概念

用C语言描述

运算

初始化

求表长

读取元素

定位

插入

删除

创建

尾插法

头插法

删除重复结点

其他链表

循环链表

双向循环链表

顺序表和链表的比较

异同

优缺点

适合场景

综合应用