第三章栈、队列和数组 - 《数据结构导论》笔记

阅读说明

本文涉及到的代码描述均为C语言。

概要

栈
1. 概念
2. 特征
3. 用C语言描述
  - 顺序栈
  - 链栈
4. 基本运算
  - 初始化
  - 栈空
  - 栈满
  - 进栈
  - 出栈
  - 取栈顶元素
5. 应用
  - 解决简单问题
队列
1. 概念
2. 特征
3. 用C语言描述
  - 顺序队列
  - 循环队列
4. 基本运算
  - 初始化
  - 队列空
  - 队列满
  - 入队列
  - 出队列
  - 取队列首元素
5. 应用
  - 解决简单问题
数组
1. 一维和二维数组
  - 逻辑结构
  - 存储结构
    - 存储位置计算
2. 矩阵的压缩存储
  - 特殊矩阵
    - 对称矩阵
    - 三角矩阵
      - 上三角矩阵
      - 下三角矩阵
  - 稀疏矩阵
    - 三元组表示法
简单的综合运用

栈

概念

栈Stack可以看作是特殊的线性表，特殊性在于基本运算是线性表运算的子集，是一种运算受限的线性表。而受限是指插入和删除运算限定在表的某一端进行。

进栈：指插入运算。
出栈：指删除运算。
栈顶：允许进栈和出栈的一端。
栈底：栈顶的另一端。
空栈：不含任何数据元素的栈。
栈顶元素：处于栈顶位置的数据元素。
上溢：栈的容量已经满了，此时再进行进栈就会发生上溢。
下溢：空栈做出栈就会产生下溢，因为栈中没有任何数据元素。

栈是计算机科学中广泛使用的数据结构之一，例如：函数的嵌套调用和程序递归的处理都是用栈来实现的。

特征

栈的修改原则是后进先出（Last In First Out），好比桌面上叠放着待清洗的碗碟，收拾以后的碗碟被放在栈顶，而在栈顶的碗碟会优先得到清洗。因此又称为后进先出线性表，简称后进先出表。

生活中的例子

具有栈特征的生活场景：

购物篮：顾客往购物篮放商品会放在栈顶，结账时从栈顶取出商品。
购物推车：顾客的购物车在结账完以后会被回收，叠放在栈顶，下一个顾客需要时会从栈顶取出。
射击：先装的子弹最后才被打出来，特殊子弹夹除外，例如左轮。
添饭：新加的米饭放在栈顶，栈顶的米饭先吃。
水杯加水：这个例子可能不太严谨，因为水流动的特性也有可能喝到非栈顶的水。

实现

栈的实现有两种方式：

顺序栈：用一组连续的存储单元存放数据元素，通常用一个一维数组和一个记录栈顶位置的变量来实现顺序存储。
链栈：用带头结点的单链表实现，命名LS（linkStack），LS指向头结点，LS->next指向栈顶结点，也是首结点，尾结点是栈底结点，通过各结点的指针连接组成栈。

栈的基本运算的功能描述：

初始化InitStack(S)：构造一个空栈S。
判断栈空EmptyStack(S)：若为空栈返回1，否则返回0。
进栈Push(S, x)：将元素x插入栈S中，x成为栈顶元素。
出栈Pop(S)：删除栈顶元素。
取栈顶GetTop(S)：返回栈顶元素。

顺序栈

定义

顺序栈相关代码放在了ghjayce/code-example - sequence stack中，感兴趣可以clone到本地查看运行结果。

1
2
3
4
5
6
7


const int maxSize=10; // 顺序栈的容量

typedef struct sequenceStack
{
    dataType data[maxSize]; // 存储栈中数据元素的数组
    int top; // 指向栈顶位置
} seqStack;

初始化

1
2
3
4
5
6


seqStack init()
{
    seqStack stack;
    stack.top = 0;
    return stack;
}

栈空

1
2
3
4
5
6
7


int isEmpty(seqStack *stack)
{
	if (stack->top == 0) {
		return 1;
	}
	return 0;
}

栈满

1
2
3
4
5
6
7


int isFull(seqStack *stack)
{
	if (stack->top == maxSize-1) {
		return 1;
	}
	return 0;
}

进栈

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


int push(seqStack *stack, dataType x)
{
    if (isFull(stack)) {
        printf("%s\n", "栈已满");
        exit(EXIT_FAILURE);
    }
    stack->top++;
    stack->data[stack->top] = x;
    return 1;
}

出栈

1
2
3
4
5
6
7
8
9


int pop(seqStack *stack)
{
    if (isEmpty(stack)) {
        printf("%s\n", "栈空");
        exit(EXIT_FAILURE);
    }
    stack->top--;
    return 1;
}

取栈顶元素

1
2
3
4
5
6
7
8


dataType getTop(seqStack *stack)
{
    if (isEmpty(stack)) {
        printf("%s\n", "栈空");
        exit(EXIT_FAILURE);
    }
    return stack->data[stack->top];
}

双栈

为了节省空间，可以让两个数据元素类型一致的栈共享同一个一维数组空间，这种做法使一维数组空间构成了双栈。

两个栈的栈底分别设在数组的两端，栈顶分别用top1、top2表示，两个栈分别做进栈运算时，彼此会迎面增长，那么判断为上溢的条件为：$top+1=top2$。

上溢条件为什么是top+1？

假设数组长度为40，0-19是第一个栈的空间范围，20-39是第二个栈的空间范围，而19+1则会超出第一个栈的空间范围，出现上溢。

双栈示意图，待补充..

用C语言表示双栈的数据结构：

1
2
3
4
5
6


const int maxSize = 40;
typedef struct doubleStack
{
	dataType data[maxSize];
	int top1, top2;
} doubleStack;

双栈运算，待补充..

链栈

定义

链栈相关代码放在了ghjayce/code-example - link stack中，感兴趣可以clone到本地查看运行结果。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


typedef struct
{
    int id;
} dataType;

typedef struct node
{
    dataType data;
    struct node *next;
} linkStack;

初始化

1
2
3
4
5
6


linkStack *init()
{
    linkStack *stack = (linkStack *)malloc(sizeof(linkStack));
    stack->next = NULL;
    return stack;
}

栈空

1
2
3
4
5
6
7


int isEmpty(linkStack *stack)
{
    if (stack->next == NULL) {
        return 1;
    }
    return 0;
}

进栈

1
2
3
4
5
6
7


void push(linkStack *stack, dataType x)
{
    linkStack *newNode = (linkStack *)malloc(sizeof(linkStack));
    newNode->data = x;
    newNode->next = stack->next;
    stack->next = newNode;
}

出栈

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


int pop(linkStack *stack)
{
    if (!isEmpty(stack)) {
        linkStack *removeNode = stack->next;
        stack->next = removeNode->next;
        free(removeNode);
        return 1;
    }
    return 0;
}

取栈顶元素

1
2
3
4
5
6
7


dataType *getTop(linkStack *stack)
{
    if (isEmpty(stack)) {
        return NULL;
    }
    return &(stack->next->data);
}

应用

1、将链栈中的结点进行逆置

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


linkStack *reverse(linkStack *stack)
{
    linkStack *newStack = init();
    linkStack *stackNode = stack->next;
    while (stackNode != NULL) {
        push(newStack, stackNode->data);
        stackNode = stackNode->next;
    }
    stackNode = stack->next;
    while (!isEmpty(newStack)) {
        dataType *data = getTop(newStack);
        if (data != NULL) {
            stackNode->data = *data;
            pop(newStack);
        }
        stackNode = stackNode->next;
    }
    return stack;
}

思路：

遍历（逐个访问链表元素）要逆置的链栈（称为A链栈）的结点，将结点通过进栈的方式放到新的链栈（称为B链栈）中，此时B链表中结点的顺序已经与A链栈相反。
对B链栈进行逐一出栈，将出栈的结点按A链表的顺序对结点进行覆盖，完成逆置。

2、递归和栈，用递归实现阶乘函数

待补充…

练习

1、设栈S的初始状态为空，若元素a、b、c、d、e、f依次进栈，得到的出栈序列是b、d、c、f、e、a，则栈S的容量至少是多少？

答：至少3。

a进，b进，容量2。
b出，容量1。
c进，d进，容量3。
d出，c出，容量1。
e进，f进，容量3。
f出，e出，a出，容量0。

2、设一个链栈的输入序列为A、B、C，试写出所得到的所有可能得输出序列。

答：共有5种可能的输出序列。

输出ABC，A进，A出，B进，B出，C进，C出。
输出ACB，A进，A出，B进，C进，C出，B出。
输出BAC，A进，B进，B出，A出，C进，C出。
输出BCA，A进，B进，B出，C进，C出，A出。
输出CBA，A进，B进，C进，C出，B出，A出。

3、有一个整数序列，其输入顺序为20，30，90，-10，45，78，试利用栈将其输出序列改变为30，-10，45，90，78，20，试给出该整数序列进栈和出栈的操作步骤，用push(x)表示x进栈，pop(x)表示x出栈。

答：

push(20)，20
push(30)，20、30
pop(30)，20
push(90)，20、90
push(-10)，20、90、-10
pop(-10)，20、90
push(45)，20、90、45
pop(45)，20、90
pop(90)，20
push(78)，20、78
pop(78)，20
pop(20)

队列

概念

队列Queue，和栈一样可以看作是特殊的运动受限的线性表，受限在于插入和删除分别在两端进行。

入队列：在队列尾部进行插入运算。
出队列：在队列首部进行删除运算。
队列首元素：队列首部第一个数据元素。
队列尾元素：队列尾部最后一个数据元素。

队列也是计算机科学中广泛使用的数据结构之一，例如：操作系统中进程调度、网络管理中的打印服务等都是用队列来实现的。

特征

队列的修改原则是先进先出（First In First out），就像排队一样，但不允许插队，新加入的成员只能排在队列尾部，先加入的成员先离开队伍。

生活中的例子

排队做核酸。
银行办业务。
排队上车/登机等。

实现

队列也有两种存储实现方式：

顺序队列：由一个一维数组以及两个分别指向队列首部元素和队列尾部元素的指针。
链队列：由一个带头结点的单链表实现，头指针front指向链表的头结点，头结点的next指向队列首结点，尾指针rear指向队列的尾结点。

队列的基本运算的功能描述：

队列初始化InitQueue(Q)：设置一个空队列Q。
判断队列为空EmptyQueue(Q)：若队列Q为空，返回1，否则返回0。
入队列EnQueue(Q, x)：将数据元素x从队尾一段插入队列。
出队列OutQueue(Q)：删除队列首元素。
取队列首元素GetHead(Q)：返回队列首元素的值。

顺序队列

定义

1
2
3
4
5
6
7


const int maxSize = 20;
typedef struct sequenceQueue
{
	dataType data[maxSize];
	int front, rear;
} seqQueue;
seqQueue SQ;

front表示队列首部，rear表示队列尾部，默认值均为0，也就是指向数组的0下标，该位置不存放数据元素。

那么入队列的操作核心关键是：

1
2


SQ.rear = SQ.rear+1;
SQ.data[SQ.rear] = x;

出队列的操作：

1

SQ.front = SQ.front+1;

这里出队列并不会去删除队列首元素，而是移动指向队列首部的指针。

但是会存在一个问题，举一个例子：

a)为空队列，SQ.rear指向0的下标，SQ.front指向0的下标。
b)为20入队后，SQ.rear指向下标1，SQ.front为0。
c)为入队列30、40、50后的队列，SQ.rear为4，SQ.front为0。
d)为出队列20、30、40、50后的队列，SQ.rear为4，SQ.front为4。
e)为入队列60后，SQ.rear为5，SQ.front为4。

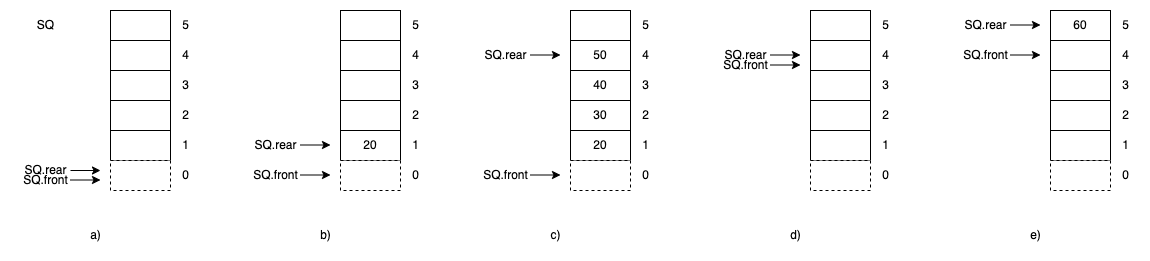
顺序队列的假溢出问题

如果在e)的状态下，要做入队列的操作，SQ.rear将会超出数组下标的范围，也就是新元素没有办法入队列，但是1-4的位置明明是空的，数组的实际空间并没有被占满，这就是假溢出现象。

另外还有一个问题是，队列空和队列满没有办法区分，就如a)和d)的情况。

循环队列

为了解决顺序队列的假溢出问题，于是就有了循环队列，它将顺序队列数组的首尾进行相接，形成了一个环状，思路就是当入队列操作SQ.rear即将要超出数组下标范围的时候，将SQ.rear=0进行重置，也就是SQ.data[0]作为新的队列尾，这样新的元素就能够利用上空闲的空间，达到循环使用。

至于没有办法区分队列空和队列满的解决方法有两种：

为队列另设一个标志，也就是多加一个变量用作区分。
队列少用一个元素空间，当只剩最后一个空间时就认为队列满，也就是CQ.rear差一步就要追上CQ.front，如图b)，书中采用了该解决方法。

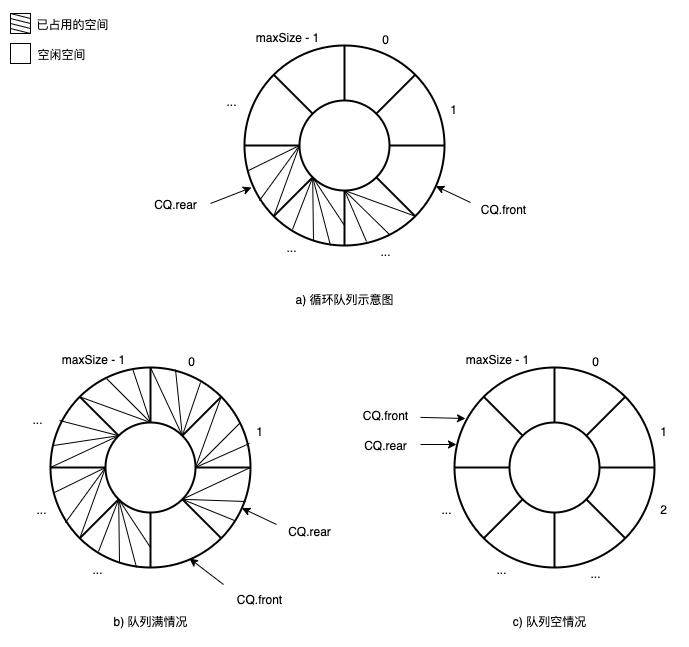
循环队列、队列满和队列空示意图

循环队列的环状让我想起了MySQL redo log的checkpoint和write pos。

定义

循环队列相关代码放在了ghjayce/code-example - cycle queue中，感兴趣可以clone到本地查看运行结果。

1
2
3
4
5
6


typedef struct cycleQueue
{
	dataType data[maxSize];
	int front, rear;
}
cycleQueue CQ;

按以上的解决思路，以下是几个操作的关键核心：

入队列的操作：

1
2


CQ.rear = (CQ.rear + 1) % maxSize;
CQ.data[CQ.rear] = x;

出队列的操作：

1

CQ.front = (CQ.front + 1) % maxSize;

队列满的条件：

1

(CQ.rear + 1) % maxSize == CQ.front;

队列空的条件：

1

CQ.rear == CQ.front;

初始化

1
2
3
4
5


void init(cycleQueue CQ)
{
	CQ.front = 0;
	CQ.rear = 0;
}

判断队列空

1
2
3
4
5
6
7


int isEmpty(cycleQueue CQ)
{
	if (CQ.front == CQ.rear) {
		return 1;
	}
	return 0;
}

入队列

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


int push(cycleQueue CQ, dataType x)
{
	if ((CQ.rear + 1) % maxSize == CQ.front) {
		printf("\s\n", "队列满");
		exit(EXIT_FAILURE);
	}
	CQ.rear = CQ.rear + 1;
	CQ.data[CQ.rear] = x;
	return 1;
}

出队列

1
2
3
4
5
6
7
8


int pop(cycleQueue CQ)
{
	if (isEmpty(CQ)) {
		return 0;
	}
	CQ.front = (CQ.front + 1) % maxSize;
	return 1;
}

取队列首元素

1
2
3
4
5
6
7
8


dataType getHead(cycleQueue *CQ)
{
    dataType data;
    if (isEmpty(CQ)) {
        return data;
    }
    return CQ->data[(CQ->front + 1) % maxSize];
}

为什么是CQ->front + 1？

上面有提到过，别忘了数组的第0个位置是不使用的，而front默认所指向的位置是0，即front所指向的空间是不存储元素的或者即使有也是已被出队列的元素。

链队列

再重复一遍，链队列是一个带有头结点的单链表组成，队列首部的指针指向头结点，头指针指向首结点，队列尾部的指针指向尾结点，队列空的时候，队列首部和尾部的指针均指向头结点。

链接的实现需要动态申请内存空间，所以不会出现队列满的情况。

定义

链队列相关代码放在了ghjayce/code-example - link queue中，感兴趣可以clone到本地查看运行结果。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


typedef struct
{
    int id;
} dataType;
typedef struct linkQueueNode
{
    dataType data;
    struct linkQueueNode *next;
} linkQueueNode;
typedef struct linkQueue
{
    linkQueueNode *front, *rear;
} linkQueue;

初始化

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


linkQueue *init()
{
	linkQueue *LQ = (linkQueue *)malloc(sizeof(linkQueue));
	// 生成队列的头结点
	linkQueueNode *node = (linkQueueNode *)malloc(sizeof(linkQueueNode));
	LQ->front = node;
	LQ->rear = node;
	(LQ->front)->next = NULL;
	reutrn LQ;
}

判断队列空

1
2
3
4
5
6
7


int isEmpty(linkQueue LQ)
{
	if (LQ.rear == LQ.front) {
		return 1;
	}
	return 0;
}

入队列

1
2
3
4
5
6
7
8


void push(linkQueue *LQ, dataType x)
{
    linkQueueNode *newNode = (linkQueueNode *)malloc(sizeof(linkQueueNode));
    newNode->data = x;
    newNode->next = NULL;
    (LQ->rear)->next = newNode;
    LQ->rear = newNode;
}

出队列

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


void pop(linkQueue *LQ)
{
    if (isEmpty(LQ)) {
        printf("%s\n", "队列空");
        exit(EXIT_FAILURE);
    }
    linkQueueNode *deleteNode = LQ->front->next;
    LQ->front->next = deleteNode->next;
    if (deleteNode->next == NULL) {
        LQ->rear = LQ->front;
    }
    free(deleteNode);
}

取队列首元素

1
2
3
4
5
6
7
8


dataType *getHead(linkQueue *LQ)
{
    if (isEmpty(LQ)) {
        return NULL;
    }
    linkQueueNode *node = LQ->front->next;
    return &(node->data);
}

应用

待补充…

数组

概念

数组array可以看成是线性表的一种推广，由一组相同类型的数据元素组成，并存储在一组连续的存储单元中。

一维数组：又称向量。
二维数组：一维数组中的数据元素是一维数组，一般写成a[m][n]，可看作由m行n列组成的线性表。
三维数组：一维数组中的数据元素是二维数组。
n维数组：一维数组中数据元素为n-1维数组。

运算

通常只有两种基本运算：

读：返回指定下标的数据元素。
写：修改指定下标的数据元素。

存储结构

一维数组数据元素的内存地址是连续的，而二维数组的数据元素有两种存储方法：

以列序为主序的存储。
以行序为主序的存储，C语言编译数组采用的正是该方法。

存储结构演示和数组的逻辑结构插图.png（待补充…）

计算存储位置

有一个二维数组a[m][n]，每个数据元素占用k个存储单元大小，以行为主序，数组元素a[i][j]的存储位置是多少？要怎么计算？

m：行数量。
n：列数量。
i：在m行的下标。
j：在n列的下标。

下标是从0开始，那么数据元素a[i][j]：

该下标之前总共有：n * i + j + 1个数据元素，其中：
- 每行有n（列的数量）个元素。
- 在第i行，有i行元素，在第j列，有j+1个元素。
第一个元素a[0][0]与a[i][j]相差n * i + j + 1 - 1个位置。

a[i][j]的存储位置计算公式为： $$loc[i, j] = loc[0, 0] + (n * i + j) * k$$ 实战一下，例如：

有一个二维数组a[10][20]，每个数据元素占用2个存储大小，数组的起始内存地址为2000，求：

a[5][10]的存储位置是多少？
- 整理数据：
  - m：10。
  - n：20。
  - i：5。
  - j：10。
  - k：2。
- 将数据套入公式：2000 + (20 * 5 + 10) * 2，存储位置最终为：2220。
a[8][19]呢？交给你来试试。

矩阵的压缩存储

待补充…

特殊矩阵

对称矩阵

如果一个n阶的方阵满足以下条件，则是一个对称矩阵：

$a_{ij} = a_{ji}$
$0 \leq i, j \leq n - 1$

三角矩阵

稀疏矩阵

应用

1、对一个$N{\times}N$阶的矩阵A进行逆置，请设计出算法。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


void MM(int A[n][n])
{
	int i, j, temp;
	for (i = 0; i < n; i++) {
		for (j = 0; j < i; j++) {
			temp = A[i][j];
			A[i][j] = A[j][i];
			A[j][i] = temp;
		}
	}
}

综合运用

待补充…

目录

阅读说明

概要

栈

概念

特征

生活中的例子

实现

顺序栈

定义

初始化

栈空

栈满

进栈

出栈

取栈顶元素

双栈

链栈

定义

初始化

栈空

进栈

出栈

取栈顶元素

应用

练习

队列

概念

特征

生活中的例子

实现

顺序队列

定义

循环队列

定义

初始化

判断队列空

入队列

出队列

取队列首元素

链队列

定义

初始化

判断队列空

入队列

出队列

应用

数组

概念

运算

存储结构

计算存储位置

矩阵的压缩存储

特殊矩阵

对称矩阵

三角矩阵

稀疏矩阵

应用

综合运用