第四章树和二叉树 - 《数据结构导论》笔记

阅读说明

涉及知识点

数学知识
- 对数

概要

树
1. 概念
  - 结构
  - 森林
  - 相关术语和计算
2. 基本运算的功能描述
二叉树
1. 概念
  - 左、右子树
2. 基本运算
3. 性质特征
  - 满二叉树
  - 完全二叉树
4. 存储结构
  - 顺序存储
  - 链式存储
5. 用C语言描述
6. 遍历算法
  - 递归实现
    - 先序遍历
    - 中序遍历
    - 后序遍历
  - 层次遍历
  - 非递归实现
树和森林
1. 树的存储结构
  - 孩子链表表示法
  - 孩子兄弟链表表示法
  - 双亲表示法
2. 树、森林和二叉树的关系与转换
  - 树转二叉树
  - 森林转二叉树
  - 二叉树转森林
3. 遍历
4. 判定树和哈夫曼树
  - 概念
    - 判定树
    - 哈夫曼树
    - 哈夫曼编码
  - 分类和判定树的关系
  - 哈夫曼树构造过程
  - 哈夫曼算法

树

概念

树Tree是一种树形结构，它是由n(n≥0)个结点组成的有限集合。

特征：树形结构结点之间具有一对多的关系，一个结点可以有一个或多个直接后继。

什么是树？

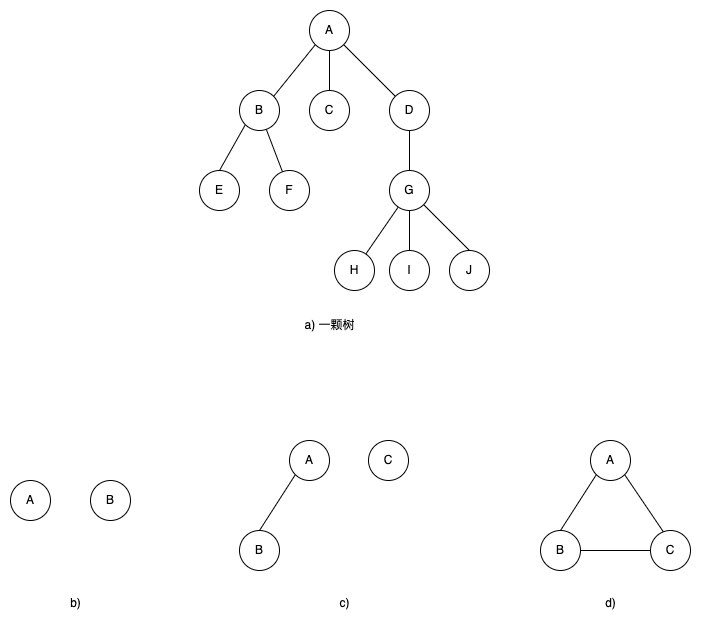
双亲：指父结点，parent node翻译过来的意思。
- 例，如图a)：
  - A没有双亲。
  - B、C、D的双亲是A。
  - E、F的双亲是B。
直接孩子：指结点的孩子，孩子的孩子不算，只是为了方便区分，一般简称孩子。
- 例，如图a)：
  - A的孩子有B、C、D。
  - B的孩子有E、F。
祖先：沿着某个结点向上追溯，直到根结点结束，路径上的所有结点都是祖先。
- 例，如图a)：
  - A没有祖先。
  - B的祖先是A。
  - H的祖先分别是G、D、A。
子孙：除了根结点以外的其他结点。
- 例，如图a)：
  - B的子孙分别是E、F。
  - D的子孙分别是G、H、I、J。
兄弟结点：某个结点的直接孩子们，它们之间是兄弟关系，拥有同一个父结点。
- 例，如图a)：
  - B、C、D它们之间是兄弟。
  - E、F是兄弟。
叶子：没有孩子的结点，也称叶子结点、终端结点。
- 例，如图a)：E、F、C、H、I、J都是叶子。
子树：某个结点的所有子孙（后代结点）所构成的树结构。
- 例，如图a)：
  - D、G、H、I、J所构成的树结构是根结点A的子树。
  - C不算子树，因为它没有子孙。
  - B、E、F这棵树是根结点A的子树。
结点的度：某一个结点有多少个直接孩子。
- 例，如图a)：
  - A结点的度为3。
  - B结点的度为2。
  - D结点的度为1。
树的度：结点的度的最大值，也就是所有结点里直接孩子最多的那个。
- 例，如图a)：树的度为3。
结点的层次：把一棵树比作一个层级金字塔，从根结点为1，每下一层+1，数到结点所在的层级。
- 例，如图a)：
  - B的层次是2。
  - E的层次是3。
  - H的层次是4。
树的高度/深度：结点的层次的最大值，也就是树一共有多少层。
- 例，如图a)：树高为4。
有序树：结点的孩子之间的按照一定的顺序排序，典型的例子是二叉树。
无序树：结点的孩子之间的顺序可以任意排列，典型的例子是普通树，也称自由树。

一棵树需要满足的条件：

当n=0时，称为空树。
当n>0时：
- 仅有一个称为根的结点，简称根结点。
- 根结点有它的直接孩子，构成父子关系，直接孩子也有自己的孩子，构成根结点的子树。
- 孩子之间没有关联，互不相交，把孩子作为一个单独的根结点时，以上条件同样适用。

上图b)、c)不是一棵树，存在两个根节点，d)也都不是一棵树，因为孩子之间相交了。

以上第2个条件是我个人方便理解的总结，贴上书上原话：有且仅有一个称为根的结点，除根节点外，其余结点分为m(m≥0)个互不相交的非空集合T₁，T₂，…，T_m，这些集合中的每一个都是一棵树，称为根的子树。

森林Forest是m(m≥0)棵互不相交的树的集合，简单点说就是有多棵树，且它们之间互不相交，例如图b)、c)。

基本运算的功能描述

求根Root(T)：求树T的根节点。
求双亲Parent(T, X)：求结点X在树T上的双亲节点，若X是根结点或不在T上，则返回特殊标志。
求孩子Child(T, X, i)：求结点X的第i个孩子结点，若X不在T上或X上没有i孩子，则返回特殊标志。
建树Create(X, T₁, …, T_k)，k>1：建立一棵以X为根，以T₁，…，T_k为第1，…，k棵子树的树。
剪枝Delete(T, X, i)：删除树T上结点X的第i棵子树，若T无第i棵子树，则为空操作。
遍历TraverseTree(T)：遍历树，即访问树中每个结点，且每个结点仅被访问一次。

二叉树

概念

二叉树Binary Tree是n(n≥0)个元素的有限集合，即在树的基础上，一棵二叉树需要满足其中一个条件：

空树，什么结点都没有。
只有一个根结点，即左右子树均为空。
右子树为空。
左子树为空。
由一个根结点和两棵互不相交的左子树和右子树组成，子树之间是有次序关系的，且均是一棵二叉树。

二叉树

$$图4.2$$

性质特征

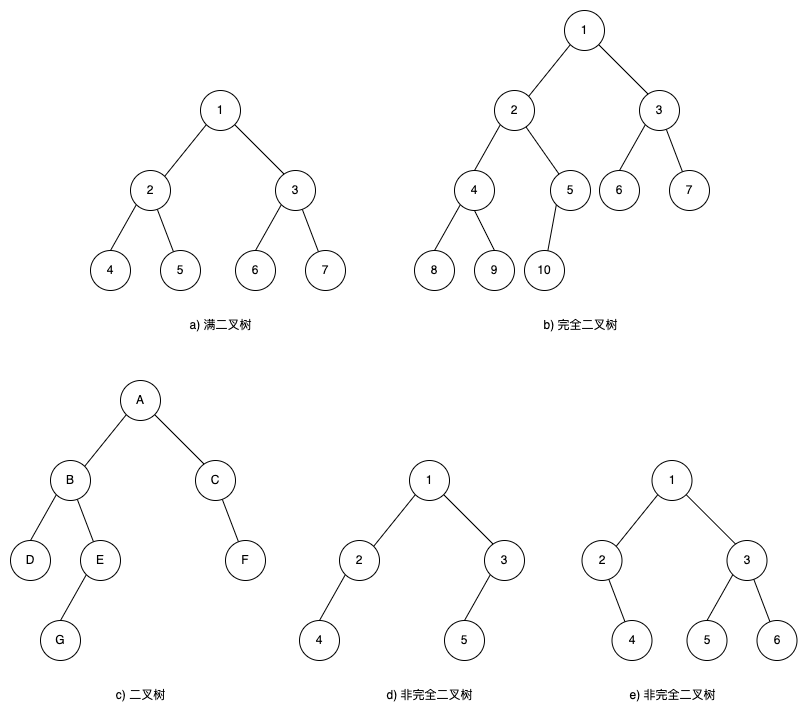
二叉树的5个性质特征：

性质1：二叉树第i（i≥1）层上至多有2^i-1个结点，也就是：
- 第一层最多有1个结点。
- 第二层最多有2个结点。
- 第三层最多有4个结点。
- 第四层最多有8个结点，以此类推。
性质2：深度为k（k≥1）的二叉树至多有2^k-1个结点，也就是例如二叉树高为3，那么最多有4个结点。
- 符合该性质的称为满二叉树。
性质3：对任何一棵二叉树，若度数为0的结点个数为$n_0$，度数为2的结点个数为$n_2$，则 $n_0=n_2+1$。
- 例如上图c)，度数为0的结点个数是3（D、G、F），度数为2的结点个数是2（A、B）。

完全二叉树：如果对满二叉树按从上到下，从左到右的顺序编号，并在树的最后一层删去部分结点（最后一层至少还剩一个结点），删完以后整棵树的结点还是顺序的排列，这就是棵完全二叉树，其性质有：

性质4：含有n个结点的完全二叉树的深度为$⌊log_2n⌋+1$。
- 其中⌊x⌋表示不大于x的最大整数，即向下取整函数，指⌊$log_2n$⌋，$log_2n$是对数，什么是对数？
- 例如上图b)，共有10个结点，即⌊log₂10⌋+1，对数结果是3.32..向下取整后是3，最终深度是4。
性质5：按上面完全二叉树的定义对结点进行顺序编号，对任意一编号为i(1 ≤ i ≤ n)的结点x，性质有：
- 若i = 1，结点x是根。
- 若i > 1，结点x的双亲的编号为：⌊i / 2⌋。
- 若2 * i ＞ n，结点x无左和右孩子；若有左孩子，其编号为2 * i。
- 若2 * i + 1 ＞ n，结点x无右孩子，若有右孩子，其编号为2 * i + 1。

书上原话：二叉树不是完全二叉树，满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。

基本运算的功能描述

初始化Initiate(BT)：建立一棵空二叉树，BT=∅。
求双亲Parent(BT, X)：找出结点X的双亲结点，若X是根结点或X不在BT上，返回NULL。
求左孩子Lchild(BT, X)：求X结点的左孩子，若X是叶子结点或X不在BT上，返回NULL。
求右孩子Rchild(BT, X)：与求左孩子逻辑一样，区别是求X结点的右孩子。
建二叉树Create(BT)：建立一棵二叉树BT。
先序遍历PreOrder(BT)：按先序对二叉树BT进行遍历，每个结点仅被访问一次。BT为空不操作。
中序遍历InOrder(BT)：与先序遍历逻辑一样，区别是以中序进行。
后序遍历PostOrder(BT)：与先序遍历逻辑一样，区别是以后序进行。
层次遍历LevelOrder(BT)：按层从上往下，每层从左往右对二叉树进行遍历，每个结点仅被访问一次。BT为空不操作。

存储结构

二叉树通常有两种存储结构：顺序存储和链式存储结构。

顺序存储

二叉树的顺序存储可以用一维数组来实现，按照性质5的特性，对结点进行从上到下从左到右的顺序进行编号，从根结点1开始，将结点顺序地存进数组的对应下标位置，下标0不使用。

顺序存储分为两种情况：

如果二叉树是完全二叉树，如下图a)、b)的方式进行存储。
如果二叉树非完全二叉树：
1. 首先必须用某种方法将其转换成完全二叉树。
2. 对不存在的结点的位置可增设虚拟结点（阴影表示）的方式，如下图e)。
3. 对应虚拟结点下标的位置使用特殊记号∧表示。

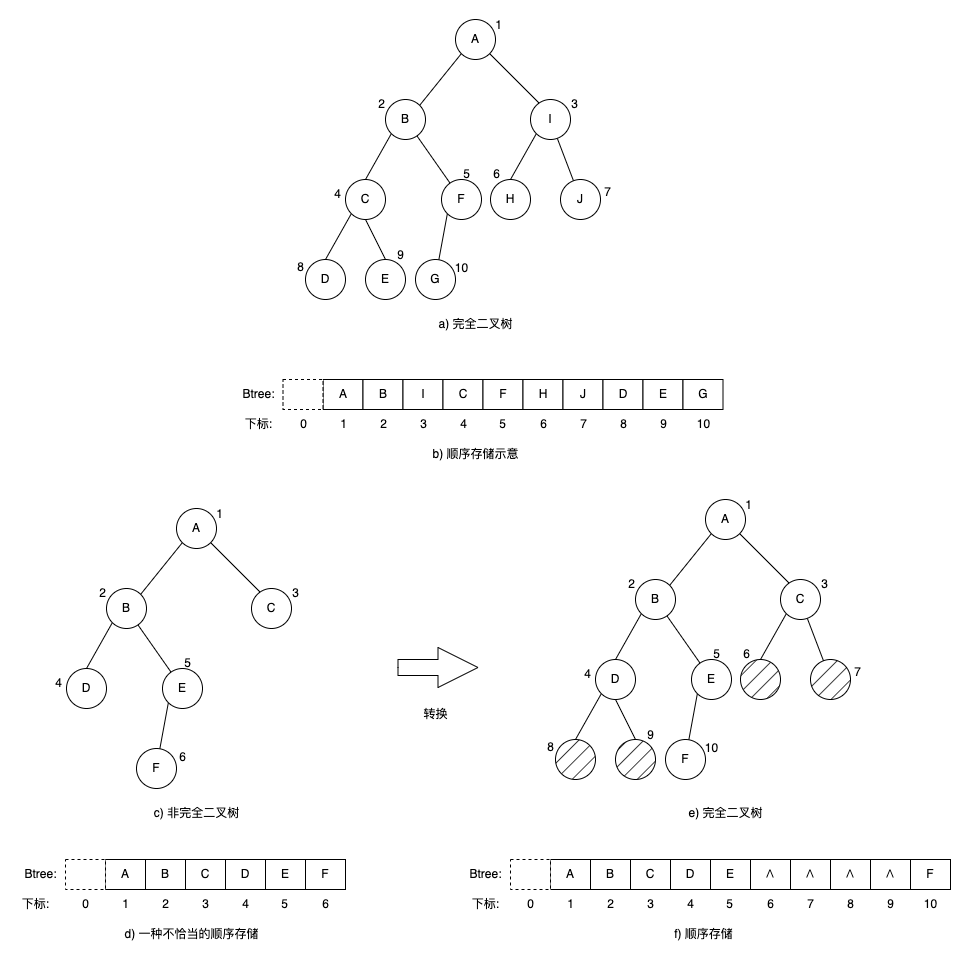
完全二叉树的顺序存储

非完全二叉树的顺序存储虽然可以用转换完全二叉树，以完全二叉树的顺序存储进行处理，这样只要是一棵二叉树（不管是哪种类型）都能够用同一种运算方式进行处理，但这种方法最大的缺点是造成了空间的浪费。

链式存储

二叉树最常用的是链式存储结构，其中又分为二叉链表和三叉链表。

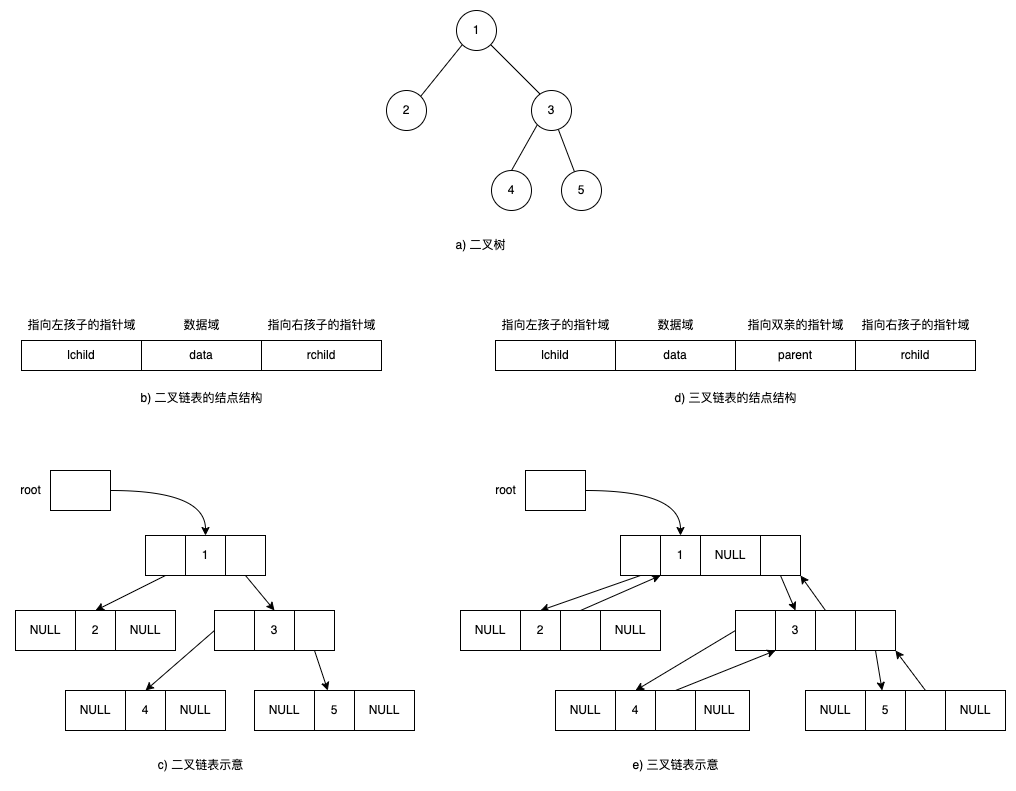
二叉树的链式存储

其中：

lchild表示指向左孩子的指针，即左指针。
- 没有左孩子时左指针域的值为NULL。
rchild表示指向右孩子的指针，即右指针。
- 没有右孩子时右指针域的值为NULL。
每个二叉链表必须有一个指向根结点的指针，即根指针，例如上图 c) 中的root，与链表头指针类似。
- 访问二叉链表只能从根指针开始。
- 若二叉树为空，则root = NULL。
三叉链表在每个结点增加了一个指针域parent，用于指向该结点的双亲。
因此总结出规律，在具有 n 个结点的二叉树中，有2n个指针域：
- 其中只有n - 1个用来指向结点的左、右孩子。
- 其余的n + 1个指针域为NULL。

用C语言描述

二叉树

1
2
3
4
5


typedef struct binaryTreeNode
{
	dataType data;
	struct binaryTreeNode *lchild, *rchild;
} *binaryTree;

三叉树

1
2
3
4
5
6


typedef struct TBNode
{
	dataType data;
	struct TBNode *lchild, *parent, *rchild;
} *ThreeBinaryTree;
ThreeBinaryTree root;

遍历

二叉树的遍历是指按某种次序访问二叉树上的所有结点，且每个结点仅访问一次。

一棵二叉树由三部分组成：根、根的左子树、根的右子树。

因此遍历二叉树总共有三个步骤：

访问根结点。
遍历根的左子树。
遍历根的右子树。

遍历共有三种次序，不同的次序只是三个步骤的顺序不同：

下面会以图4.2中的c)二叉树为例，分别说明对应次序的序列。

先序遍历。
- 步骤顺序，简记为：根左右。
  - 访问根结点。
  - 先序遍历根的左子树。
  - 先序遍历根的右子树。
- 先序遍历结点的序列为：ABDEGCF，以下是遍历过程：
  1. 访问A。
  2. 先序遍历A的左子树（BDEG）。
    1. 访问B。
    2. 先序遍历B的左子树（D）。
      1. 访问D。
      2. 先序遍历D的左子树（空）。
      3. 先序遍历D的右子树（空）。
    3. 先序遍历B的右子树（EG）。
      1. 访问E。
      2. 先序遍历E的左子树（G）。
        
        访问G。
        
        先序遍历G的左子树（空）。
        
        先序遍历G的右子树（空）。
      3. 先序遍历E的右子树（空）。
  3. 先序遍历A的右子树（CF）。
    1. 访问C。
    2. 先序遍历C的左子树（空）。
    3. 先序遍历C的右子树（F）。
      1. 访问F。
      2. 先序遍历F的左子树（空）。
      3. 先序遍历F的右子树（空）。
中序遍历。
- 步骤顺序，简记为：左根右。
  - 中序遍历根的左子树。
  - 访问根结点。
  - 中序遍历根的右子树。
- 结点的序列为：DBGEACF。
后序遍历。
- 步骤顺序，简记为：左右根。
  - 后序遍历根的左子树。
  - 后序遍历根的右子树。
  - 访问根结点。
- 结点的序列为：DGEBFCA。

递归实现

先序、中序和后序都是基于递归的实现，下面给出各次序具体的算法。

假设visit(bt)函数是访问指针bt所指结点。

先序遍历

1
2
3
4
5
6
7
8


void preorder(binaryTree bt)
{
	if (bt != NULL) {
		visit(bt);
		preorder(bt->lchild);
		preorder(bt->rchild);
	}
}

中序遍历

1
2
3
4
5
6
7
8


void inorder(binaryTree bt)
{
	if (bt != NULL) {
		inorder(bt->lchild);
		visit(bt);
		inorder(bt->rchild);
	}
}

后序遍历

1
2
3
4
5
6
7
8


void postorder(binaryTree bt)
{
	if (bt != NULL) {
		postorder(bt);
		postorder(bt);
		visit(bt);
	}
}

层次遍历

不是重点，待补充…

非递归实现

不是重点，待补充…

应用

1、根据先序遍历和中序遍历次序创建一棵二叉树。

先序遍历次序：ABDEGCF。
中序遍历次序：DBGEACF。

算法：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


binaryTree createByPreInOrder(char preArr[], char inArr[], int preArrMinIndex, int preArrMaxIndex, int inArrMinIndex, int inArrMaxIndex)
{
    if (inArrMaxIndex < 0) {
        return NULL;
    }
    int k;
    // 如下申请内存的方式出自书上，是高度概括的，会存在内存越界导致结果出现一些不可预料的问题。
    // binaryTree bt = malloc(sizeof(binaryTree));
    // 以下是正确的申请方式，两者之间在64位机器上相差16字节，前者8字节，后者24字节
    binaryTree bt = malloc(sizeof(struct binaryTreeNode));
    bt->data.val = preArr[preArrMinIndex];
    k = inArrMinIndex;
    while ((k <= inArrMaxIndex) && (inArr[k] != preArr[preArrMinIndex])) {
        k++;
    }
    if (k > inArrMaxIndex) {
        return NULL;
    }
    bt->lchild = createByPreInOrder(preArr, inArr, preArrMinIndex + 1, preArrMinIndex + k - inArrMinIndex, inArrMinIndex, k - 1);
    bt->rchild = createByPreInOrder(preArr, inArr, preArrMinIndex + k - inArrMinIndex + 1, preArrMaxIndex, k + 1, inArrMaxIndex);
    return bt;
}

实现思路：

以递归的方式，逐个将先序遍历次序的结点在中序遍历次序范围中查找，简称在中序遍历中找根结点。
找到根节点以后，在中序遍历次序中分出该根节点的左子树（根结点的左边）和右子树（根结点的右边）的范围。
- 以A根结点为例，在中序遍历次序中：
  - A的左子树即DBGE。
  - A的右子树即CF。
在左子树和右子树的范围中，再重复步骤1，在范围中寻找先序遍历次序的下一个结点，从而得到完整的左右子树。

2、根据中序遍历和后序遍历次序创建一棵二叉树。

中序遍历次序：BACDEFGH。
后序遍历次序：BCAEDGHF。

思路：与先序遍历和中序遍历一样，都是从中序遍历中找到左右子树。

步骤：

由后序遍历次序确定F是根结点，那么在中序遍历次序中，F的左子树是BACDE，右子树是GH。
- 即得出后序遍历次序中，BCAED是F的左子树，GH是F的右子树。
那么从后序遍历次序的左子树范围中确定左子树的根结点是D，重复步骤1。
- 在中序遍历次序中：
  - D的左子树是：BAC。
  - D的右子树是：E。
- 在后序遍历次序中即：
  - D的左子树是：BCA。
  - D的右子树是：E。
继续下一个根节点A，A的左孩子是B，右孩子树C。
回到F的右子树：GH，H是根结点，H的左孩子是G。

算法：

待补充…

树和森林

树的存储结构

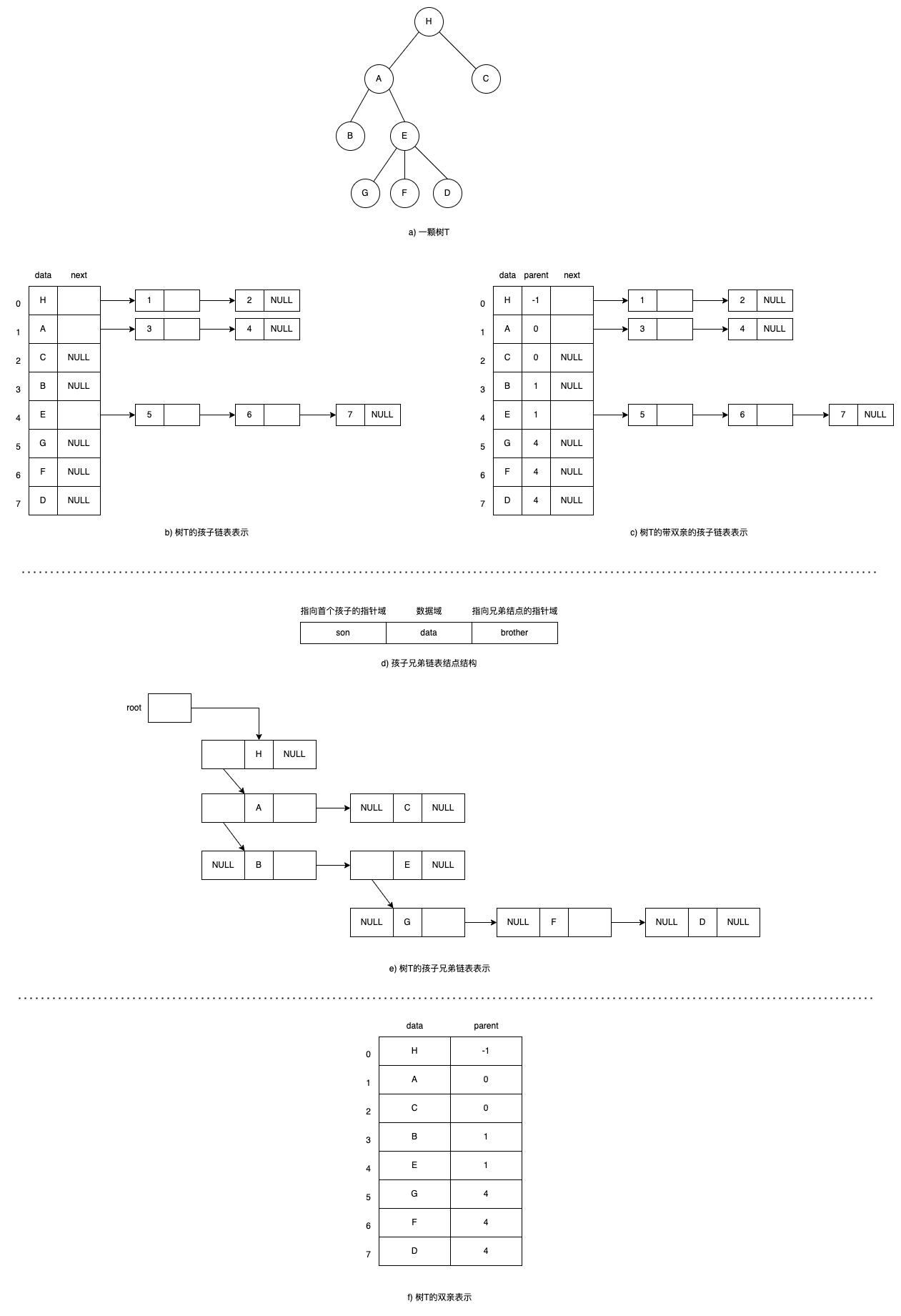
树的存储结构示例图

$$图4.5$$

孩子链表表示法

用C语言表示：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


const int MAX_NODE_NUM = 20;

typedef struct dataType
{
	char val;
} dataType;

typedef struct node
{
	int index;
	struct node *next;
} *childLink;

typedef struct childLinkArr
{
	dataType data;
	childLink firstChild;
} childLinkArr;

int main() {
	childLinkArr link[MAX_NODE_NUM];
	return 0;
}

结合C语言定义和上图b)所示，其中：

childLinkArr是一个数组，数组元素个数与上图a)树T的结点的数量相同，结点存放的顺序按树T从上到下从左到右依次排列。
数组元素由数据域 + 首个孩子指针域组成。
- 数据域：用于存放结点值。
- 首个孩子指针域：指向从左到右的第一个孩子。
- 首个孩子指针域可以看作是头结点，其所指向的孩子链表（childLink）是一个单链表，分别是结点的第一个孩子、第二个孩子、第三个孩子以此类推。
孩子链表也由数据域 + 指针域组成。
- 数据域：存放孩子在数组childLinkArr中的下标位置。
- 指针域：指向下一个孩子，也是当前孩子的兄弟结点。

为了便于找到双亲，对childLinkArr结构体改进一下：

增加一个双亲域parentIndex，存储结点双亲在数组childLinkArr中的下标位置，如上图c)。

用C语言表示：

1
2
3
4
5
6


typedef struct childLinkArr
{
	dataType data;
	childLink firstChild;
	int parentIndex;
} childLinkArr;

孩子兄弟链表表示法

如上图d)、e)所示，孩子兄弟链表的结构表示形式和二叉链表完全相同，只是结点含义不同：

二叉链表，当前结点分为左孩子指针和右孩子指针。
孩子兄弟链表，当前结点分为首个左孩子指针（简称孩子指针）和兄弟结点指针，剩下的孩子通过遍历孩子指针的兄弟结点指针找到。

用C语言表示：

1
2
3
4
5


typedef struct brotherNode
{
	dataType data;
	struct brotherNode *son, *brother;
} *treeLink;

双亲表示法

如上图f)所示，是当中存储结构最简单的一种，同样也是采取数组的方式，由数据域+双亲域组成：

数据域：将树T所有的结点按从上到下从左到右的顺序，结点从下标0开始，一一存进数组。
双亲域：存储双亲结点在数组中的下标位置，没有双亲存储-1。

用C语言表示：

1
2
3
4
5
6
7


const int size = 10;
typedef struct
{
	dataType data;
	int parentIndex;
} Node;
Node treeParentArr[size];

疑问：

只靠双亲怎么知道有哪些孩子？以及孩子的顺序？
- 答：
  - 双亲parentIndex是同一个值的，就表示这些都是孩子。
  - 因为存储已经按从左到右顺序存储，把同一个双亲的所有结点找出来，数组下标的顺序就是孩子直接的顺序，即保证了孩子之间的逻辑结构。

树、森林和二叉树之间的转换

树转换成二叉树

转换方法：

加线，所有兄弟结点之间加一条线，彼此连接起来。
抹线，除了结点的第一个左孩子，其他孩子与结点的连线全部抹掉。
旋转，以根节点为轴心，对树进行顺时针的适当旋转。

森林转换成二叉树

转换方法：

将森林中的每棵树转换成二叉树。
加线，转换以后的二叉树，从第二棵二叉树开始，将其根节点作为前一棵二叉树根结点的右子树，以此类推。

二叉树转换成森林

转换方法：

抹线，断开根结点与右孩子的连线，此时得到两棵二叉树。
抹线再加线，二叉树根节点的左子树的右子树们均断开连接，改成均与根节点之间连接，如果根节点有右子树，重复步骤1的操作。
剩下的二叉树重复按以上步骤进行处理。

树和森林的遍历

树

以图4.5的a)树为例。

先序遍历

访问根结点
从左往右依次遍历孩子，以孩子为根节点，重复步骤1和步骤2。

先序遍历次序为：HABEGFDC。

后序遍历

后序遍历根的孩子子树。
访问根结点。

后序遍历次序：BGFDEACH。

层次遍历

访问根结点。
逐层往下遍历，每层从左到右依次访问结点。

层次遍历次序：HACBEGFD。

森林

森林有两种遍历方法：

先序遍历

从左到右访问第一棵树的根结点。
先序遍历根结点的子树。
先序遍历森林中的其他树，重复以上步骤。

中序遍历

从左到右中序遍历第一棵树根结点的第一个孩子的子树。
访问第一棵树的根节点。
中序遍历剩下的孩子的子树。
中序遍历森林中的其他树，重复以上步骤。

判定树和哈夫曼树

分类和判定树

树有广泛的应用，其中一种重要的应用是描述分类的过程。

分类是一种常用的运算，将输入数据按照标准划分成不同的种类，例如：

类别	A	B	C	D
年龄值 age	age < 18	18 ≤ age ＜ 45	45 ≤ age ＜ 60	age ≥ 60
百分比	0.2	0.3	0.25	0.25

插图..

用于描述分类过程的二叉树称为判定树，其中上图a)的分类算法为：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


char classify(int age)
{
	if (age < 18) {
		return 'A';
	} else if (age < 45) {
		return 'B';
	} else if (age < 60) {
		return 'C';
	} else {
		return 'D';
	}
}

假设人口有N=10000人，C类别人口占25%，根据a)的判断树，区分1个人是否属于C类别需要进行3次比较，那么10000个人就需要$10000 \times 0.25 \times 3$，即7500次。

所有类别总共需要的比较次数就是：23000次。

1
2
3
4


SUM = (N × 0.2 × 1) + (N × 0.3 × 2) + (N × 0.25 × 3) + (N × 0.25 × 3)
    = N × (0.2 + 0.6 + 0.75 + 0.75)
    = 10000 × 2.3
    = 23000

平均比较次数是：$SUM \div N$ 即$23000 \div 10000 = 2.3$次。

而如果是b)的判断树，区分1人属于C类别则只需要2次比较，10000个人则需要5000次。

所有类别总共需要比较20000次。

1
2
3
4


SUM = (N × 0.2 × 2) + (N × 0.3 × 2) + (N × 0.25 × 2) + (N × 0.25 × 2)
    = N × (0.4 + 0.6 + 0.5 + 0.5)
    = 10000 × 2
    = 20000

平均比较次数是2次，相较a)，总共减少了3000次比较，平均比较次数减少了0.3次。

这说明，按不同判定树进行分类的计算量是不同的，有时可以相差很大，怎样才能构造出像b)一样，平均比较次数最少的判定树呢？

没错，可以用到哈夫曼树和哈夫曼算法。

哈夫曼树和哈夫曼算法

以上面的例子为例，给定一组权值为{p₁, …, p_k}的序列，如何构造出一棵有k个叶子结点分别以权为值的判定树，并且平均比较次数是最小的？

步骤如下：

根据一组权值为{p₁, …, p_k}的序列，构造森林F={T₁, …, T_k}，其中T_i是一棵只有根结点，权为p_i的二叉树。
- 如图a)。
从F中选取两个权最小的两棵二叉树，组成一棵新的二叉树，左右孩子分别是两个权最小的二叉树
- 如图b)。
从F中删掉步骤2已经合并的两棵二叉树，并将新的二叉树加入F，如图c)。
此时再看是否还有多个二叉树。
- 如果是，继续重复步骤2。
- 直到只剩下一棵二叉树，这棵二叉树就是哈夫曼树，如图d)。

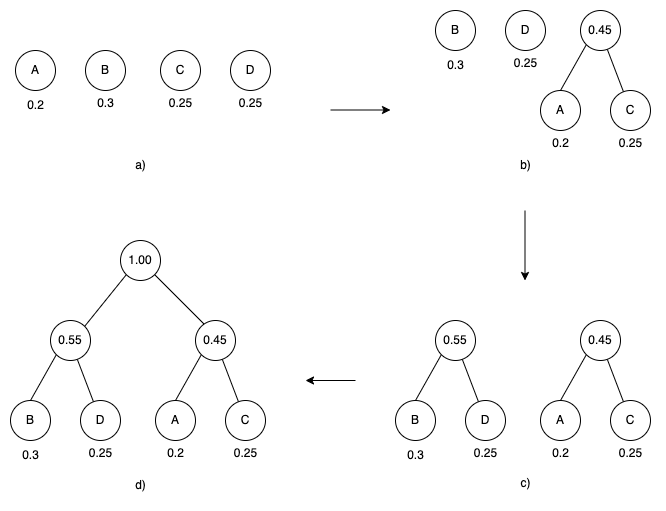
哈夫曼树构建过程

从中得出规律：

需要经过$n-1$次合并，最终得出一棵哈夫曼树，其中n是指权值的数目，以上面的例子，权值数目为4。
最终得到的哈夫曼树共有$2n-1$个结点，其中：
- 哈夫曼树没有度数为 1 的分支结点。

用C语言实现，即哈夫曼算法，采用顺序存储，大小是2n-1的数组，数组中的元素有四个域，分别是：

权值。
双亲下标值。
左孩下标值。
右孩下标值。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49


#include <float.h>

const int n = 10;
typedef struct
{
    float weigh;
    int parent, lchild, rchild;
} node;

typedef node huffmanTree[2*n-1];

void huffman(int size, float weigh[], huffmanTree tree)
{
    int index, j, x, y;
    float m, n;
    // 初始化
    for (index = 0; index < 2 * k - 1; index++) {
        tree[index].parent = -1;
        tree[index].lchild = -1;
        tree[index].rchild = -1;
        if (index < size) {
            tree[index].weigh = weigh[index];
        } else {
            tree[index].weigh = 0;
        }
    }
    for (index = 0; index < size - 1; index++) {
        x = 0;
        y = 0;
        m = FLT_MAX;
        n = FLT_MAX;
        for (j = 0; j < size + index; j++) {
            if ((tree[j].weigh < m) && (tree[j].parent == -1))  {
                n = m;
                y = x;
                m = tree[j].weigh;
                x = j;
            } else if ((tree[j].weigh < n) && (tree[j].parent == -1)) {
                n = tree[j].weigh;
                y = j;
            }
        }
        tree[x].parent = size + index;
        tree[y].parent = size + index;
        tree[size + index].weigh = m + n;
        tree[size + index].lchild = x;
        tree[size + index].rchild = y;
    }
}

哈夫曼编码

在通信领域中，通常希望字符在传输过程中总的编码长度越短越好，即对字符的存储进行压缩，能否找到最短的编码方案呢？

没错，还是哈夫曼树，不过要加点编码。

思路：

通过对字符出现次数进行统计，字符是值，权是出现次数或者叫出现频率。
让出现频率较多的字符采用较短的编码。
出现频率较少的字符采用较长的编码。

哈夫曼二叉树的每个结点的左分支标记为0，右分支为1（如下图f)），这样，从根结点到每个叶子结点的路径，把路径所在的分支标记全部加起来就是对应字符的编码，这些编码就称为哈夫曼编码。

例如：某个通信系统需要传输一个字符串”aaa bb cccc dd e“，它们出现的频率分别是：

字符	a	’’ (空)	b	c	d	e
频率	3	4	2	4	2	1

频率序列从小到大排列后是：

字符	e	b	d	a	’’ (空)	c
频率	1	2	2	3	4	4

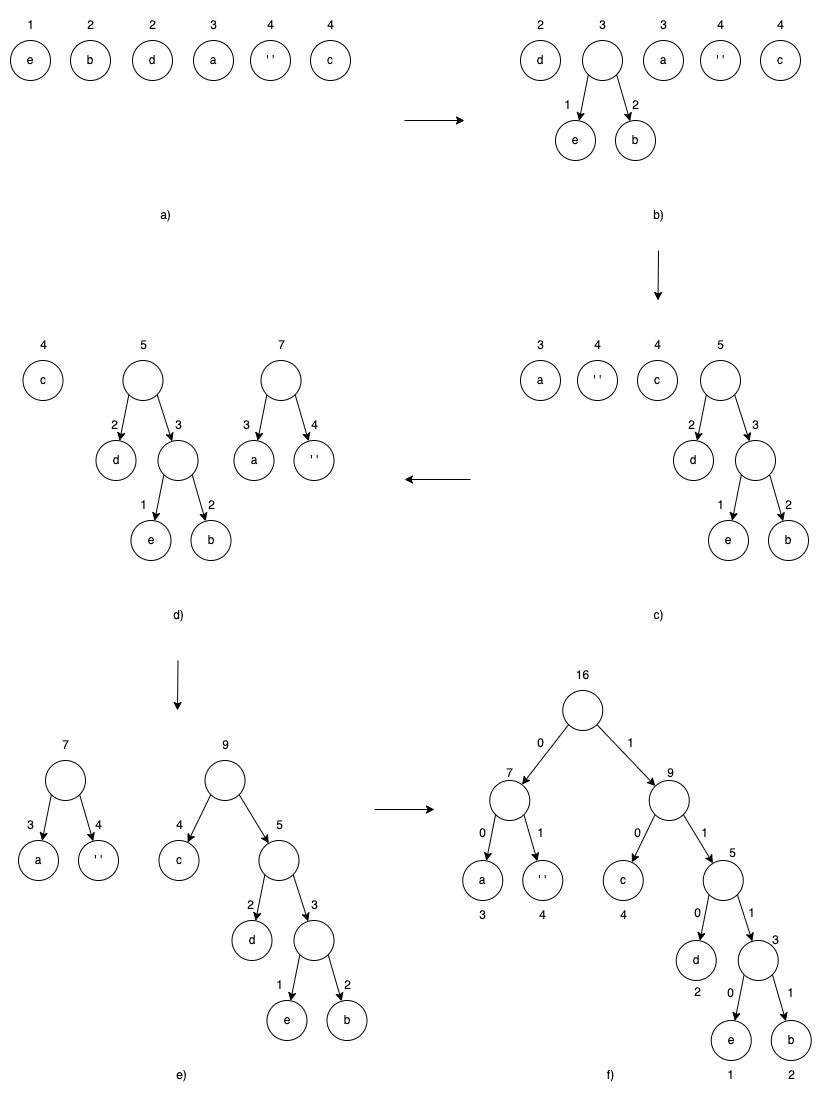
哈夫曼树编码构建过程

经过哈夫曼树编码后，如上图f)，字符对应的编码分别是：

字符	a	’’ (空)	b	c	d	e
编码	00	01	110	10	1111	1110

即字符串”aaa bb cccc dd e“对应的编码序列为”0000000111011001101010100111111111011110“。

为了方便大家查看比对，用|对每个字符编码进行分开：

1

00|00|00|01|110|110|01|10|10|10|10|01|1111|1111|01|1110

哈夫曼编码序列在还原成字符串的过程是，以上面的序列为例：

拿接下来的第一个编码，即0，在哈夫曼树中寻找。
未找到，则把第一个编码和下一个编码加在一起，即00（a），继续在哈夫曼树中寻找。
- 没找到则一直重复步骤2。
- 找到了，即拿到了编码对应的字符串。
重置这个过程，继续走步骤1，直至结束。

目录

阅读说明

涉及知识点

概要

树

概念

基本运算的功能描述

二叉树

概念

性质特征

基本运算的功能描述

存储结构

顺序存储

链式存储

用C语言描述

二叉树

三叉树

遍历

递归实现

先序遍历

中序遍历

后序遍历

层次遍历

非递归实现

应用

树和森林

树的存储结构

孩子链表表示法

孩子兄弟链表表示法

双亲表示法

树、森林和二叉树之间的转换

树转换成二叉树

森林转换成二叉树

二叉树转换成森林

树和森林的遍历

树

先序遍历

后序遍历

层次遍历

森林

先序遍历

中序遍历

判定树和哈夫曼树

分类和判定树

哈夫曼树和哈夫曼算法

哈夫曼编码

参考