第五章图 - 《数据结构导论》笔记

阅读说明

为了方便文章表述，以下内容有一些调整：

书中顶点v₀、v₁、v₂，在文中以v0、v1、v2的方式进行描述（文字以及配图）。

概要

概念

应用背景

假如有这样一个问题，在N个城市间建立通信网络，使得其中任意两个城市之间有直接或间接的通信线路，假设已知每两个城市之间通信线路的造价，要求找出一个总造价最低的通讯网络。

当N很大时，这个问题十分复杂，就需要用到计算机来求解，而使用到的数据结构就是图结构。

这里有几个需要解决的问题：

如何描述该问题的数据？
如何在计算机中存储数据？
解决问题的算法是什么？

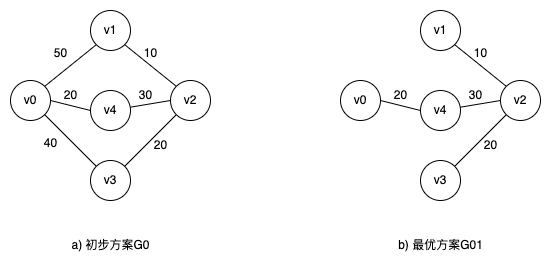
用图描述通信网络的问题

$$图1$$

顶点：即上图的圆圈。
- 如图1a)，v0、v1、v2等。
- 在上面的例子圆圈代表一个城市。
边：即上图圆圈之间的连线，也称为顶点的偶对。
- 如图1a)，v0和v1之间的连线。
权：即连线旁边的数值，也称为边的权。
- 如图1a)，v0和v1的权为50。
- 在实际应用中，权可以表示一个顶点到另一个顶点的距离、代价或耗费等。
带权图：每条边都带有权的图。
- 如图1a)。

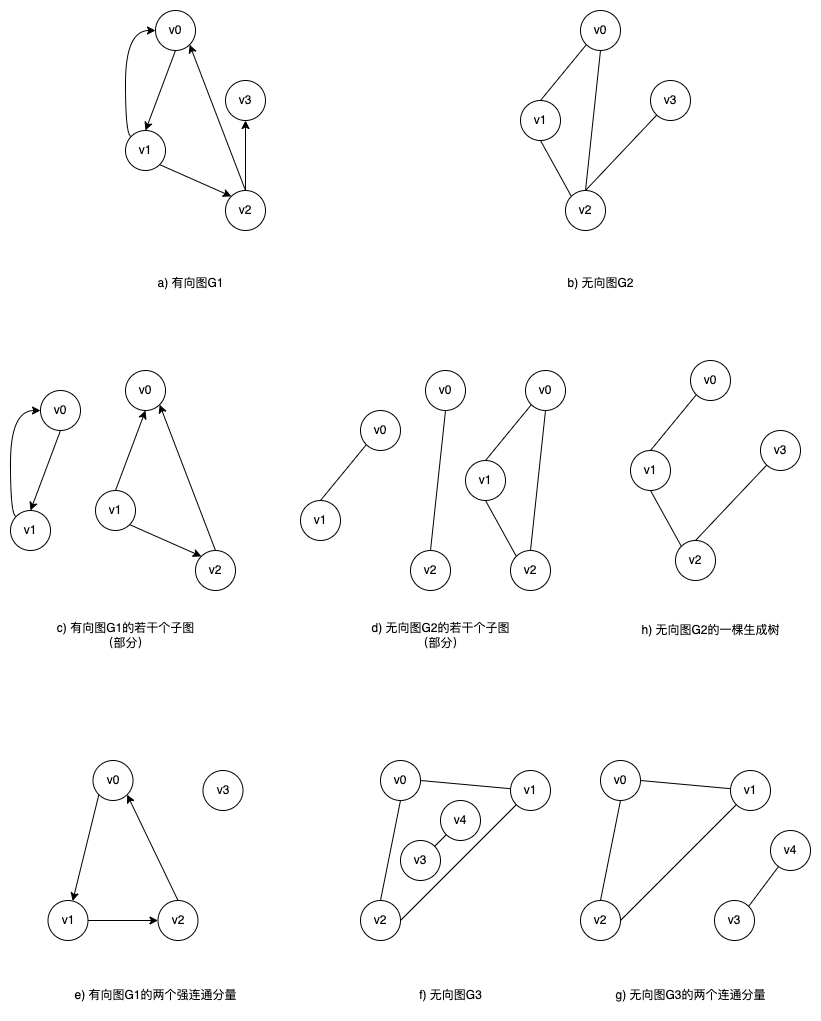
用图描述通信网络的问题

$$图2$$

图Graph由两个集合V和E组成，记为$G=(V, E)$，其中：

V是顶点的有穷非空集合，一般表示为：V = {v0, v1, v2}。
E是边的集合，一般表示为：E = {<v0, v1>, <v1, v2>}。
有向图：顶点的偶对是有序的。
- 有序偶对用尖括号括起来，例：<v0, v1>，含义是从顶点v0到顶点v1有一条边。
- 如图2a)是一个有向图，可以看到边是带有箭头的，即有方向的。
无向图：顶点的偶对是无序的。
- 无序偶对用圆括号括起来，例：(v0, v1)，含义与有向图一样。
- 如图2b)是一个无向图。
弧：有向图的边又称为弧（无向图可没有这种说法，大概用于区分的作用）。
弧头：表示弧的终点，即弧有箭头的一端。
- 例：<v0, v1>，图2a)的v0和v1的弧，v1就是弧头的一端。
弧尾：表示弧的始点/起点。
- 例：<v0, v1>，图2a)的v0和v1的弧，v0就是弧尾的一端。

无向图中(v0, v1)和(v1, v0)是同一条边，但对于有向图来说，<v0, v1>和<v1, v0>可是两条不同的弧。

有向完全图：任何两个顶点之间都有弧的有向图。
- 一个具有n个顶点的有向完全图的弧的数量为：$n(n-1)$。
  - 为什么？怎么得出来的公式？
    - 将所有顶点连接起来只需要顶点数量-1条边就足够了，例如2个顶点只需1条线，3个顶点只需2条线，因此得出n-1。
    - 而作为有向完全图来说，两个顶点都有弧则需要两条边才行，例如2个顶点需要2条线，3个顶点需要6条线，就是在上面的基准下再加多一条线，因此得出n(n - 1)。
无向完全图：任何两个顶点之间都有边的无向图。
- 一个具有n个顶点的无向完全图的边的数量为：$\frac{n(n-1)}{2}$。
  - 怎么得出来的公式？根据定义得知，无向图顶点之间的边是同一条边，即2个顶点只需要1条线，因此拿有向完全图的公式除2就能够得出无向完全图的边的数目了。
顶点的度：与该顶点相关联的边共有多少，记为D(v)。
- D全称：degree。
- v表示顶点。
- 顶点度 = 入度 + 出度之和，即D(v) = ID(v) + OD(v)。
  - 以图2a)，v2为例：
    - ID(v2) = 1。
    - OD(v2) = 2。
    - D(v2) = 3。
  - 以图2b)为例：
    - D(v1) = 2。
    - D(v2) = 3。
入度：仅有向图，以顶点为终点的弧共有多少，记为ID。
- I全称：input。
出度：仅有向图，以顶点为始点的弧共有多少，记为OD。
- O全称：output。
子图：$G=(V, E)$是一个图，若E'是E的子集，V'是V的子集，并且E'中的边仅与V'中的顶点相关联，则图$G’=(V’, E’)$称为图G的子图。
路径：从一个顶点x到另一个顶点y之间的路线，这个路径也称为顶点的序列。
- 例图2b)，无向图的顶点v0到v3的路径共有2条：
  - 顶点序列v0，v1，v2，v3，路径长度为3。
  - 顶点序列v0，v2，v3，路径长度为2。
路径长度：路径上边/弧的数目。
简单路径：序列中顶点不重复出现的路径。
- 例图2b)，顶点序列v0，v1，v2，v3就是一条简单路径。
回路：第一个顶点和最后一个顶点相同的路径，也称为环。
- 例图2b)，以下路径都是回路：
  - v0→v1→v2→v0→v2→v0
  - v0→v1→v2→v0
简单回路：除了第一个顶点和最后一个顶点外，其余顶点不重复的回路。
- 例图2b)，以下是简单回路：
  - v0→v1→v2→v0
连通：顶点x到顶点y有路径，则称顶点x和顶点y是连通的。
连通图：图中任意两个顶点都是连通的。
- 例图2b)是一个连通图。
  - v0和v3没有直接的边但也能通过v0->v2->v3进行连通，因此符合连通图的定义。
- 例图2f)是非连通图，因为存在多个不连通顶点，例如v0和v3是不连通的。
连通分量：无向图中的极大（最大）连通子图。
- 简单点说，以图2f)为例，把一个图中的所有顶点看成一个整体的图，而单独取v0、v1、v2三个顶点构成的子图来说，就像图2g)，它就是一个连通图，也是一个连通分量，它是一个整体图中的一个连通分量，包括v3和v4构成的子图也是一样是一个连通分量。

连通相关的术语是针对无向图的，而强连通相关术语就是用来描述有向图的。

强连通：与连通的含义一样，区别是无向图的连通本身就是双向的，如果是有向图，则要求顶点和顶点之间是双向相连才称为强连通。
强连通图：与连通的含义一样，任意两个顶点都是强连通的。
强连通分量：与连通分量的含义一样，不做赘述（估计是用来区分有向和无向的专业术语）。

如果极大（最大）连通子图是用来讨论分量的，那么极小（最小）连通子图就是用来讨论生成树的。

生成树：一个连通图例图2b)，含有全部顶点的一个极小连通子图就是生成树，就像例图2g)所示。
- 观察规律得知：
  - 如果连通图G的顶点数量为n，G的生成树的边数则为n-1。
  - 如果G的一个子图G’的边数大于n-1，则G’子图中一定有环。
  - 相反，如果边数小于n-1，则G’一定不连通。

特征

在图Graph结构中，任意两个结点之间都可能有关系，结点之间的邻接关系可以是任意的，即多对多的关系。

存储结构

图的存储结构有很多种：

邻接矩阵。
邻接表。
十字链表。
邻接多重表。
等等等等…。

文中主要介绍邻接矩阵和邻接表。

邻接矩阵

使用二维数组很容易就能够实现。

以<v_i, v_j>或者(v_i, v_j)为例，定义如下：

用0表示v_i和v_j之间，即偶对并没有关联。
用1表示v_i和v_j之间，即偶对存在关联。

以图2为例，有向图G1和无向图G2的邻接矩阵，M1和M2分别如下：

无向图的邻接矩阵是一个对称矩阵，有向图的邻接矩阵是一个稀疏矩阵。

配图5，p134，待补充… $$图5$$ 如图5，反映出了顶点之间的邻接关系，即逻辑关系，其中：

矩阵M1的有向图为例：
- <v₀, v₁>第0行第1列为1，表示顶点v₀和v₁之间存在关联。
- 顶点的集合是：V = {v₀, v₁, v₂, v₃}，即顶点共有4个。
- 弧的集合是：E = {<v₀, v₁>, <v₁, v₀>, <v₁, v₂>, <v₂, v₀>, <v₂, v₃>}，弧共有5条。
矩阵M2的无向图为例：
- <v₀, v₁>第0行第1列和<v₁, v₀>第1例第0行都是1，表示顶点v₀和v₁之间存在关联，注意是双向的。
  - 这两个偶对实际上是指同一条边，要和有向图区分开来。
- 顶点的集合是：V = {v₀, v₁, v₂, v₃}，即顶点共有4个。
- 边的集合是：E = {<v₀, v₁>, <v₁, v₂>, <v₀, v₂>, <v₂, v₃>}，边共有4条。

仅邻接关系还不够，用C语言完整的表示是：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


const int num = 20; // 一般为x*y数量的积
typedef struct vertexType
{
	char val;
}
typedef struct graph
{
	vertexType vexs[num]; // 顶点信息
	int matrix[num][num]; // 邻接矩阵
	int vertexNum, sideNum; // 顶点数，边数
} graph;

若是带权的邻接矩阵，则是：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


const int num = 20;
// 用于标识矩阵下没有数值的情况，值的大小按实际情况定义，只要能与权值区分开即可
const int maxNum = 32767;
typedef struct vertexType
{
	char val;
}
typedef struct weightType
{
	int weight;
} weightType;
typedef struct graph
{
	vertexType vertexs[num];
	weightType matrix[num][num];
	int vertexNum, sideNum;
} graph;

邻接表

邻接表是顺序存储与链式存储相结合的存储方法。

图的应用

最小生成树

Prim

遍历

图的遍历是指从图中的某个顶点出发，系统地访问图中的每个顶点，每个顶点仅访问一次。

图的遍历操作类似于树的遍历操作，遍历的方式有两种，且都适用于有向图和无向图：

深度优先搜索遍历，类似于树的先序遍历。
广度优先搜索遍历，类似于树的层次遍历。

由于图的顶点可能会与多个顶点相关联，在遍历过程中可能会多次访问到某个顶点，为了避免重复访问的问题，要记下每个已访问的顶点。可以用到数组，当顶点被访问后，对应下标的位置标记成1。

参考

【精选】【数据结构】连通图、连通分量与强连通图、强连通分量—区别在于强，强强在哪里？